Non-dominated Sorting Genetic Algorithm III (NSGA-III)¶
The Non-dominated Sorting Genetic Algorithm III (NSGA-III) [Deb2014]
is implemented in the deap.tools.selNSGA3() function. This example
shows how it can be used in DEAP for many objective optimization.
Problem Definition¶
First we need to define the problem we want to work on. We will use
the first problem tested in the paper, 3 objectives DTLZ2 with k = 10
and p = 12. We will use pymop
for problem implementation as it provides the exact Pareto front that we
will use later for computing the performance of the algorithm.
PROBLEM = "dtlz2"
NOBJ = 3
K = 10
NDIM = NOBJ + K - 1
P = 12
H = factorial(NOBJ + P - 1) / (factorial(P) * factorial(NOBJ - 1))
BOUND_LOW, BOUND_UP = 0.0, 1.0
problem = pymop.factory.get_problem(PROBLEM, n_var=NDIM, n_obj=NOBJ)
Algorithm Parameters¶
Then we define the various parameters for the algorithm, including the population size set to the first multiple of 4 greater than H, the number of generations and variation probabilities.
MU = int(H + (4 - H % 4))
NGEN = 400
CXPB = 1.0
MUTPB = 1.0
Classes and Tools¶
Next, NSGA-III selection requires a reference point set. The reference point set serves to guide the evolution into creating a uniform Pareto front in the objective space.
ref_points = tools.uniform_reference_points(NOBJ, P)
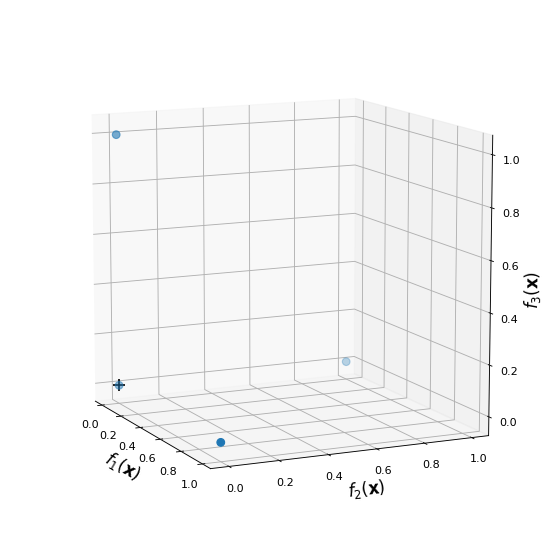
The next figure shows an example of reference point set with p = 12.
The cross represents the the utopian point (0, 0, 0).
(Source code, png, hires.png, pdf)
As in any DEAP program, we need to populate the creator with the type of individual we require for our optimization. In this case we will use a basic list genotype and minimization fitness.
creator.create("FitnessMin", base.Fitness, weights=(-1.0,) * NOBJ)
creator.create("Individual", list, fitness=creator.FitnessMin)
Moreover, we need to populate the evolutionary toolbox with initialization, variation and selection operators. Note how we provide the reference point set to the NSGA-III selection scheme.
def uniform(low, up, size=None):
try:
return [random.uniform(a, b) for a, b in zip(low, up)]
except TypeError:
return [random.uniform(a, b) for a, b in zip([low] * size, [up] * size)]
toolbox = base.Toolbox()
toolbox.register("attr_float", uniform, BOUND_LOW, BOUND_UP, NDIM)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.attr_float)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("evaluate", problem.evaluate, return_values_of=["F"])
toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=30.0)
toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=20.0, indpb=1.0/NDIM)
toolbox.register("select", tools.selNSGA3, ref_points=ref_points)
Evolution¶
The main part of the evolution is mostly similar to any other
DEAP example. The algorithm used is close to the
eaSimple() algorithm as crossover and mutation are
applied to every individual (see variation probabilities above). However,
the selection is made from the parent and offspring populations instead
of completely replacing the parents with the offspring.
def main(seed=None):
random.seed(seed)
# Initialize statistics object
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", numpy.mean, axis=0)
stats.register("std", numpy.std, axis=0)
stats.register("min", numpy.min, axis=0)
stats.register("max", numpy.max, axis=0)
logbook = tools.Logbook()
logbook.header = "gen", "evals", "std", "min", "avg", "max"
pop = toolbox.population(n=MU)
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in pop if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# Compile statistics about the population
record = stats.compile(pop)
logbook.record(gen=0, evals=len(invalid_ind), **record)
print(logbook.stream)
# Begin the generational process
for gen in range(1, NGEN):
offspring = algorithms.varAnd(pop, toolbox, CXPB, MUTPB)
# Evaluate the individuals with an invalid fitness
invalid_ind = [ind for ind in offspring if not ind.fitness.valid]
fitnesses = toolbox.map(toolbox.evaluate, invalid_ind)
for ind, fit in zip(invalid_ind, fitnesses):
ind.fitness.values = fit
# Select the next generation population from parents and offspring
pop = toolbox.select(pop + offspring, MU)
# Compile statistics about the new population
record = stats.compile(pop)
logbook.record(gen=gen, evals=len(invalid_ind), **record)
print(logbook.stream)
return pop, logbook
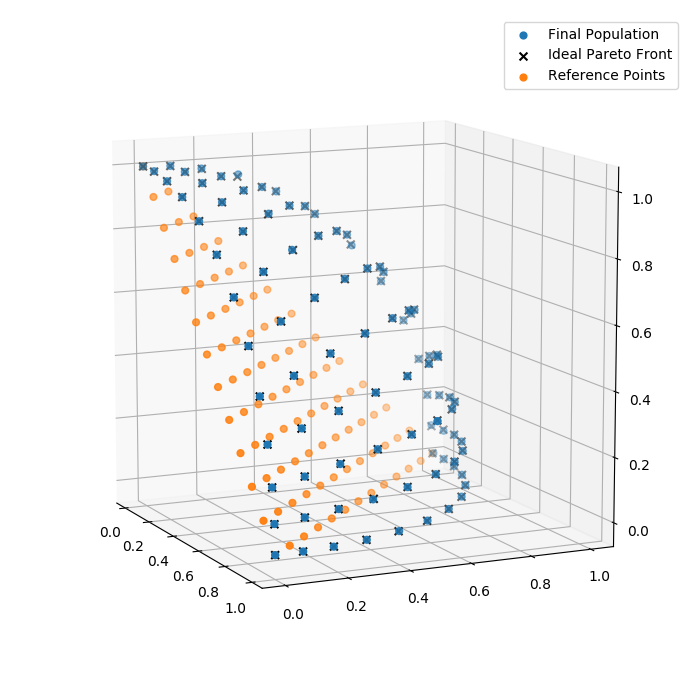
Finally, we can have a look at the final population
Higher Dimensional Objective Space¶
NSGA-III requires a reference point set that depends on the number
of objective. This point set can become quite big for even relatively
low dimensional objective space. For example, a 15 dimensional
objective space with a uniform reference point set with p = 4
would have 3060 points. To avoid this situation and reduce the
algorithms runtime [Deb2014] suggest to combine reference point
set with lower p value. To do this in DEAP, we can combine multiple
uniform point set using:
# Parameters
NOBJ = 3
P = [2, 1]
SCALES = [1, 0.5]
# Create, combine and removed duplicates
ref_points = [tools.uniform_reference_points(NOBJ, p, s) for p, s in zip(P, SCALES)]
ref_points = numpy.concatenate(ref_points, axis=0)
_, uniques = numpy.unique(ref_points, axis=0, return_index=True)
ref_points = ref_points[uniques]
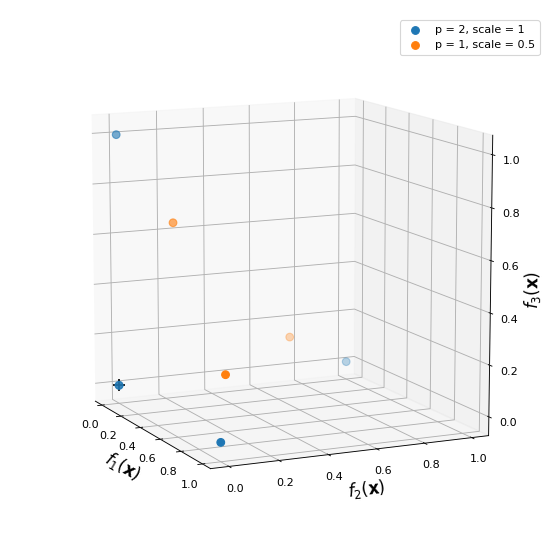
This would give the following reference point set with two underlying uniform distribution: one at full scale, and the other at half scale.
(Source code, png, hires.png, pdf)
Conclusion¶
That’s it for the NSGA-III algorithm using DEAP, now you can leverage the power of many-objective optimization with DEAP. If you’re interested, you can copy the example change the evaluation function and try applying it to your own problem.
| [Deb2014] | (1, 2) Deb, K., & Jain, H. (2014). An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Transactions on Evolutionary Computation, 18(4), 577-601. doi:10.1109/TEVC.2013.2281535. |