Genetic Programming¶
To see a given function, one can simply print out an individual candidate solution to see the string representation. However, it is possible to generate a figure.
Genetic programming is a special field of evolutionary computation that aims at building programs automatically to solve problems independently of their domain. Although there exist diverse representations used to evolve programs, the most common is the syntax tree.
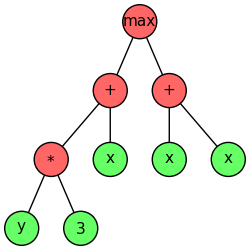
For example, the above figure presents the program \(\max(x + 3 * y, x + x)\). For this tree and further examples, the leaves of the tree, in green, are called terminals, while the internal nodes, in red, are called primitives. The terminals are divided in two subtypes: the constants and the arguments. The constants remain the same for the entire evolution while the arguments are the program inputs. For the last presented tree, the arguments are the variables \(x\) and \(y\), and the constant is the number \(3\).
In DEAP, user defined primitives and terminals are contained in a primitive set. For now, two kinds of primitive set exists: the loosely and the strongly typed.
Loosely Typed GP¶
Loosely typed GP does not enforce a specific type between the nodes. More specifically, primitives’ arguments can be any primitives or terminals present in the primitive set.
The following code define a loosely typed PrimitiveSet for the
previous tree
pset = PrimitiveSet("main", 2)
pset.addPrimitive(max, 2)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.mul, 2)
pset.addTerminal(3)
The first line creates a primitive set. Its arguments are the name of the
procedure it will generate ("main") and its number of inputs, 2. The next
three lines add functions as primitives. The first argument is the function to
add and the second argument the function arity. The last line adds a constant
terminal. Currently, the default names for the arguments are "ARG0" and
"ARG1". To change it to "x" and "y", simply call
pset.renameArguments(ARG0="x")
pset.renameArguments(ARG1="y")
In this case, all functions take two arguments. Having a 1 argument negation function, for example, could be done with
pset.addPrimitive(operator.neg, 1)
Our primitive set is now ready to generate some trees. The gp
module contains three prefix expression generation functions
genFull(), genGrow(), and
genHalfAndHalf(). Their first argument is a primitive set. They return
a valid prefix expression in the form of a list of primitives. The content of
this list can be read by the PrimitiveTree class to create a
prefix tree.
expr = genFull(pset, min_=1, max_=3)
tree = PrimitiveTree(expr)
The last code produces a valid full tree with height randomly chosen between 1 and 3.
Strongly Typed GP¶
In strongly typed GP, every primitive and terminal is assigned a specific type. The output type of a primitive must match the input type of another one for them to be connected. For example, if a primitive returns a boolean, it is guaranteed that this value will not be multiplied with a float if the multiplication operator operates only on floats.
def if_then_else(input, output1, output2):
return output1 if input else output2
pset = PrimitiveSetTyped("main", [bool, float], float)
pset.addPrimitive(operator.xor, [bool, bool], bool)
pset.addPrimitive(operator.mul, [float, float], float)
pset.addPrimitive(if_then_else, [bool, float, float], float)
pset.addTerminal(3.0, float)
pset.addTerminal(1, bool)
pset.renameArguments(ARG0="x")
pset.renameArguments(ARG1="y")
In the last code sample, we first define an if then else function that returns
the second argument if the first argument is true and the third one otherwise.
Then, we define our PrimitiveSetTyped. Again, the procedure is
named "main". The second argument defines the input types of the program.
Here, "x" is a bool and "y" is a float. The third
argument defines the output type of the program as a float. Adding
primitives to this primitive now requires to set the input and output types of
the primitives and terminal. For example, we define our "if_then_else"
function first argument as a boolean, the second and third argument have to be
floats. The function is defined as returning a float. We now understand that
the multiplication primitive can only have the terminal 3.0, the
if_then_else function or the "y" as input, which are the only floats
defined.
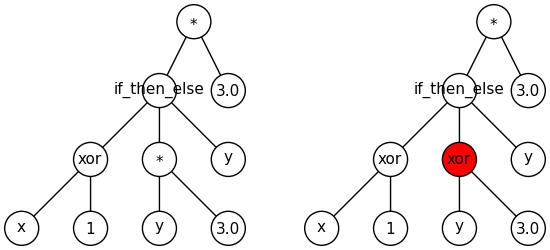
The previous code can produce the tree on the left but not the one on the right because the type restrictions.
Note
The generation of trees is done randomly while making sure type
constraints are respected. If any primitive has an input type that no
primitive and terminal can provide, chances are that this primitive will be
picked and placed in the tree, resulting in the impossibility to complete
the tree within the limit fixed by the generator. For example, when
generating a full tree of height 2, suppose "op" takes a boolean and a
float, "and" takes 2 boolean and "neg" takes a float, no terminal is
defined and the arguments are booleans. The following situation will occur
where no terminal can be placed to complete the tree.
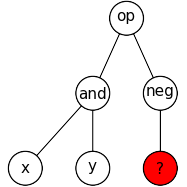
In this case, DEAP raises an IndexError with the message "The
gp.generate function tried to add a terminal of type float, but there is
none available."
Ephemeral Constants¶
An ephemeral constant is a terminal encapsulating a value that is generated from a given function at run time. Ephemeral constants allow to have terminals that don’t have all the same values. For example, to create an ephemeral constant that takes its value in \([-1, 1)\) we use
pset.addEphemeralConstant(lambda: random.uniform(-1, 1))
The ephemeral constant value is determined when it is inserted in the tree and never changes unless it is replaced by another ephemeral constant. Since it is a terminal, ephemeral constant can also be typed.
pset.addEphemeralConstant(lambda: random.randint(-10, 10), int)
Generation of Tree Individuals¶
The code presented in the last two sections produces valid trees. However, as
in the Operators and Algorithms tutorial, these trees are not yet valid individuals for
evolution. One must combine the creator and the toolbox to produce valid
individuals. We need to create the Fitness and the Individual
classes. We add a reference to the primitive set to the Individual in
addition to the fitness. This is used by some of the gp operators to modify the
individuals.
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMin,
pset=pset)
We then register the generation functions into a Toolbox.
toolbox = base.Toolbox()
toolbox.register("expr", gp.genFull, pset=pset, min_=1, max_=3)
toolbox.register("individual", tools.initIterate, creator.Individual,
toolbox.expr)
Calling toolbox.individual() readily returns an individual of type
PrimitiveTree.
Evaluation of Trees¶
In DEAP, trees can be translated to readable Python code and compiled to Python
code objects using functions provided by the gp module. The first
function, str() takes an expression or a PrimitiveTree and
translates it into readable Python code. For example, the following lines
generate a tree and output the code from the first example primitive set.
>>> expr = genFull(pset, min_=1, max_=3)
>>> tree = PrimitiveTree(expr)
>>> str(tree)
'mul(add(x, x), max(y, x))'
Now, this string represents the program we just generated, but it cannot yet be
executed. To make it executable, we have to compile the expression into a Python
code object. Since this function has two inputs, we wish to compile the code
into a callable object. This is possible with compile().
The function takes two arguments: the expression to compile and the associated
primitive set. The following example compiles the previous tree and evaluates the
resulting function for \(x=1\) and \(y=2\).
>>> function = compile(tree, pset)
>>> function(1, 2)
4
When the generated program has no input argument, the expression can be
compiled to byte code using the same compile() function.
An example of this sort of problem is the Artificial Ant Problem.
Tree Size Limit and Bloat Control¶
Since DEAP uses the Python parser to compile the code represented by the trees, it inherits from its limitations. The most commonly encountered restriction is the parsing stack limit. The Python interpreter parser stack limit is usually fixed between 92 and 99. This means that an expression can at most be composed of 91 succeeding primitives. In other words, a tree can have a maximum depth of 91. When the limit is exceeded, Python raises the following error
s_push: parser stack overflow
Traceback (most recent call last):
[...]
MemoryError
Since this limit is hard-coded in the interpreter, there exists no easy way to increase it. Furthermore, this error commonly stems from a phenomena known in GP as bloat. That is, the produced individuals have reached a point where they contain too much primitives to effectively solve the problem. This problem leads to evolution stagnation. To counteract this, DEAP provides different functions that can effectively restrain the size and height of the trees under an acceptable limit. These operators are listed in the GP section of Operators.
Plotting Trees¶
The function deap.gp.graph() returns the necessary elements to plot tree
graphs using NetworX or pygraphviz. The graph function takes a valid
PrimitiveTree object and returns a node list, an edge list and
a dictionary associating a label to each node. It can be used like following
with pygraphviz.
from deap import base, creator, gp
pset = gp.PrimitiveSet("MAIN", 1)
pset.addPrimitive(operator.add, 2)
pset.addPrimitive(operator.sub, 2)
pset.addPrimitive(operator.mul, 2)
pset.renameArguments(ARG0='x')
creator.create("Individual", gp.PrimitiveTree)
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=1, max_=2)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
expr = toolbox.individual()
nodes, edges, labels = gp.graph(expr)
### Graphviz Section ###
import pygraphviz as pgv
g = pgv.AGraph()
g.add_nodes_from(nodes)
g.add_edges_from(edges)
g.layout(prog="dot")
for i in nodes:
n = g.get_node(i)
n.attr["label"] = labels[i]
g.draw("tree.pdf")
Using NetworkX, the last section becomes:
import matplotlib.pyplot as plt
import networkx as nx
g = nx.Graph()
g.add_nodes_from(nodes)
g.add_edges_from(edges)
pos = nx.graphviz_layout(g, prog="dot")
nx.draw_networkx_nodes(g, pos)
nx.draw_networkx_edges(g, pos)
nx.draw_networkx_labels(g, pos, labels)
plt.show()
Depending on the version of graphviz, the nodes may appear in an unpredictable order. Two plots of the same tree may have sibling nodes swapped. This does not affect the primitive tree representation nor the numerical results.
How to Evolve Programs¶
The different ways to evolve program trees are presented through the Genetic Programming (GP) examples.